Hello dear Python coding buddies. It’s time to get your brain in action and solve some challenging problems. We have worked out 10 Python tricky coding exercises to be done using loops.
List of Python Tricky Coding Exercises
These exercises would require you to brainstorm, think at multiple levels, and test your coding grit to solve. However, a coding solution is provided for each of these. Let’s begin.
Exercise 1: Check If a Number is a Row in Pascal Triangle
Write a Python program that checks if a given number is a row number in Pascal’s Triangle. Pascal’s Triangle is a triangular array of binomial coefficients, where each number is the sum of the two directly above it.
Pascal’s Triangle is like a pyramid of numbers where each number is found by adding the two numbers directly above it. The triangle starts and ends with 1, and the interior numbers are the sum of the two numbers above them. It’s a way of organizing numbers that helps with binomial expansions in math.
In Pascal’s Triangle, each row contains a sequence of numbers, and these numbers are binomial coefficients. A triangular number, when associated with a row in Pascal’s Triangle, would be one of these binomial coefficients in that row.
To clarify, if a number is a triangular number, you should be able to find it in one of the rows of Pascal’s Triangle. It will be one of the numbers in that particular row. That’s what we’ll be doing to identify a number as the row in the triangle.
Example:
Input: 6
Output: True (6 is a row number in Pascal's Triangle)Solution:
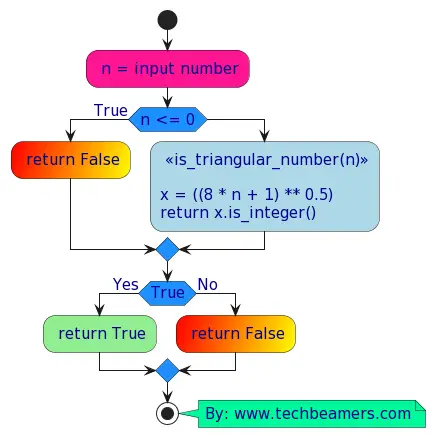
def find_pascal_row_index(n):
"""
Finds the row index in Pascal's Triangle where a given number is located.
Args:
n: The number to search for.
Returns:
A tuple (found, row_index), where `found` is True if the number is found, False otherwise,
and `row_index` is the row index if the number is found, -1 otherwise.
"""
# Handle negative and zero cases
if n <= 0:
return (False, -1)
# Check if n is a valid row number in Pascal's Triangle
row_index = find_triangular_number_index(n)
return (row_index != -1, row_index + 2) # Adding 2 to adjust for the 0-based indexing
def find_triangular_number_index(num):
"""
Finds the row index in Pascal's Triangle for a given triangular number.
Args:
num: The triangular number to search for.
Returns:
The row index if the triangular number is found, -1 otherwise.
"""
# A number is triangular if 8 * num + 1 is a perfect square
sqrt_result = int((8 * num + 1) ** 0.5)
# Check if the square root result is an integer
if sqrt_result ** 2 == 8 * num + 1:
# The row index is half of the square root result minus 1
return (sqrt_result - 1) // 2
else:
return -1
def print_result(num, found, index):
print(f"{'True' if found else 'False'}, Number {num} is {'found' if found else 'not found'} at {'row' if found else 'any'} index: {index if found else 'None'}")
def print_pascals_triangle(max_row):
"""
Prints Pascal's Triangle up to the specified row number.
Args:
max_row: The highest row number to print Pascal's Triangle up to.
"""
for row in range(max_row):
pascal_row = get_pascal_row(row)
print(f"Row {row + 1}: {' '.join(map(str, pascal_row)).center(max_row * 3)}")
def get_pascal_row(row):
"""
Generates a row of Pascal's Triangle.
Args:
row: The row number to generate.
Returns:
A list representing the row of Pascal's Triangle.
"""
result = [1]
for i in range(1, row + 1):
result.append(result[-1] * (row - i + 1) // i)
return result
# Test cases
found, index = find_pascal_row_index(3)
print_result(3, found, index)
found, index = find_pascal_row_index(5)
print_result(5, found, index)
found, index = find_pascal_row_index(6)
print_result(6, found, index)
found, index = find_pascal_row_index(7)
print_result(7, found, index)
found, index = find_pascal_row_index(8)
print_result(8, found, index)
found, index = find_pascal_row_index(10)
print_result(10, found, index)
found, index = find_pascal_row_index(15)
print_result(15, found, index)
print()
# Print Pascal's Triangle up to the highest row number (in this case, 10)
print_pascals_triangle(10)The above code first checks whether the input number is a triangular number by using this formula (8 * num + 1) ** 0.5. After that, it looks for its row index in the Pascal triangle. We tested the code with multiple inputs and tried to print the results with detail. Moreover, a full triangle is also displayed so that you can cross-check the result visually.
Exercise 2: Check If a 2D List Forms Magic Square in Python
Write a Python program that checks if a given 2D list forms a magic square. In a magic square, the sum of numbers in each row, column, and main diagonals is the same.
Example:
matrix = [
[2, 7, 6],
[9, 5, 1],
[4, 3, 8]
]
Output: True (Forms a magic square)Solution:
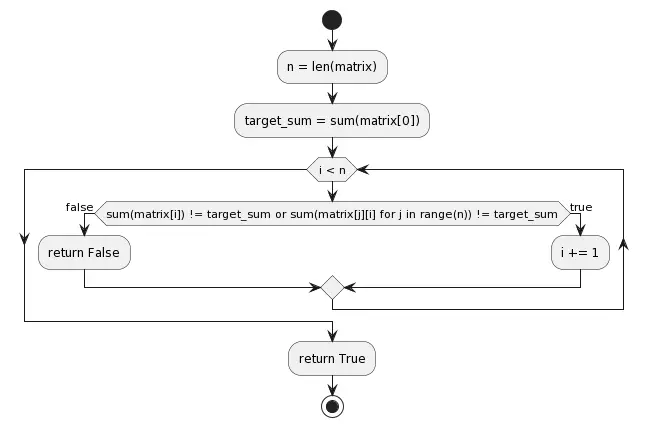
def is_magic_square(matrix):
n = len(matrix)
target_sum = sum(matrix[0])
# Check rows and columns
for i in range(n):
if sum(matrix[i]) != target_sum or sum(matrix[j][i] for j in range(n)) != target_sum:
return False
# Check main diagonal
if sum(matrix[i][i] for i in range(n)) != target_sum:
return False
# Check secondary diagonal
if sum(matrix[i][n - i - 1] for i in range(n)) != target_sum:
return False
return True
# Test cases
test_cases = [
{
"matrix": [
[2, 7, 6],
[9, 5, 1],
[4, 3, 8]
],
"expected_output": True
},
{
"matrix": [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
],
"expected_output": False,
"explanation": "Sum of rows, columns, and diagonals is not the same."
},
{
"matrix": [
[16, 23, 17],
[78, 32, 21],
[17, 16, 15]
],
"expected_output": True
},
{
"matrix": [
[1, 1, 1],
[2, 2, 2],
[3, 3, 3]
],
"expected_output": False,
"explanation": "Each number in the square is not distinct."
}
]
for case in test_cases:
matrix = case["matrix"]
expected_output = case["expected_output"]
result = is_magic_square(matrix)
explanation = case.get("explanation", "")
print(f"Matrix: {matrix}, Output: {result}, Expected: {expected_output}, Explanation: {explanation}")Exercise 3: Generate NxN Spiral of Prime Numbers in Python
Write a Python program that generates a spiral of prime numbers. The program should take a positive integer n and output an n x n matrix with prime numbers arranged in a spiral pattern.
Example:
Input: 4
Output:
[
[7, 8, 9, 10],
[6, 1, 2, 11],
[5, 4, 3, 12],
[16, 15, 14, 13]
]Solution:
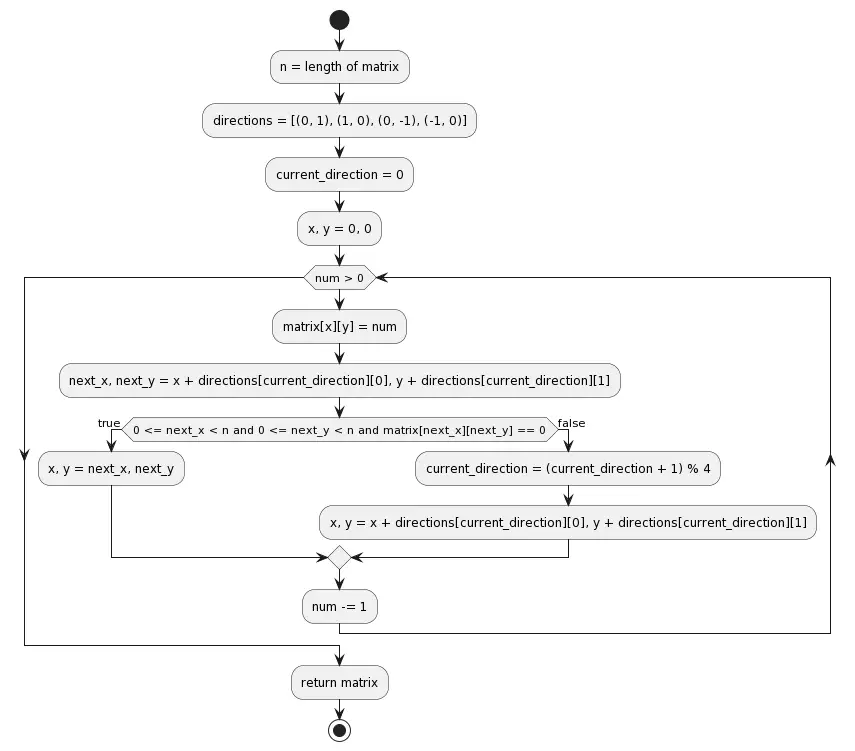
def generate_prime_spiral(n):
matrix = [[0] * n for _ in range(n)]
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
current_direction = 0
x, y = 0, 0
for num in range(n * n, 0, -1):
matrix[x][y] = num
next_x, next_y = x + directions[current_direction][0], y + directions[current_direction][1]
if 0 <= next_x < n and 0 <= next_y < n and matrix[next_x][next_y] == 0:
x, y = next_x, next_y
else:
current_direction = (current_direction + 1) % 4
x, y = x + directions[current_direction][0], y + directions[current_direction][1]
return matrix
# Test
result = generate_prime_spiral(4)
for row in result:
print(row)These exercises involve intricate patterns and require careful consideration of loop structures and mathematical concepts. They aim to test problem-solving skills and the ability to work with loops effectively.
Let’s continue with a few more challenging and tricky Python coding exercises. They will push you to think critically and carefully. Each exercise involves a unique problem that requires creative solutions.
Exercise 4: Find the Number of Unique Paths in a MxN Grid
You are given a grid with m rows and n columns. Starting from the top-left corner, you can move either down or right at any point in time. Write a Python program to find the number of unique paths to the bottom-right corner.
Example:
Input: m = 3, n = 7
Output: 28Solution:
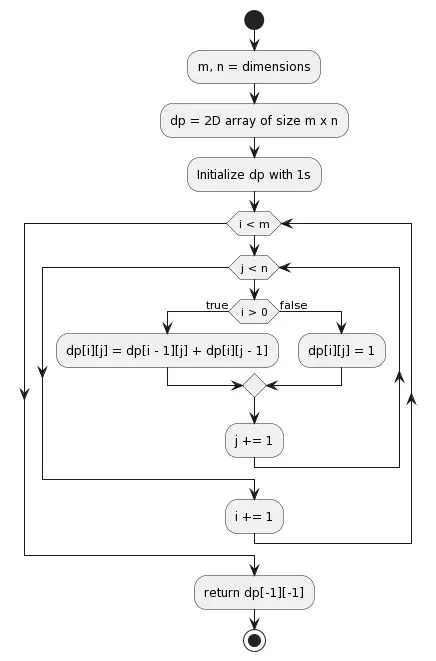
def unique_paths(m, n):
dp = [[1] * n for _ in range(m)]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[-1][-1]
def test_unique_paths(test_cases):
for test_case in test_cases:
m, n, expected_output = test_case
result = unique_paths(m, n)
print(f"Input: m = {m}, n = {n}\nOutput: {result}\nExpected: {expected_output}\n{'Pass' if result == expected_output else 'Fail'}\n")
# Test cases
test_cases = [
(3, 7, 28),
(3, 3, 6),
# Add more test cases as needed
]
# Run the tests
test_unique_paths(test_cases)Exercise 5: Find Out the Largest Square in a 2D Binary Matrix
Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
Such a matrix is also known as a binary maximal square by definition has the most and same no. of rows and columns with 0’s and 1’s.
Example:
Input:
matrix = [
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
Output: 4Solution:
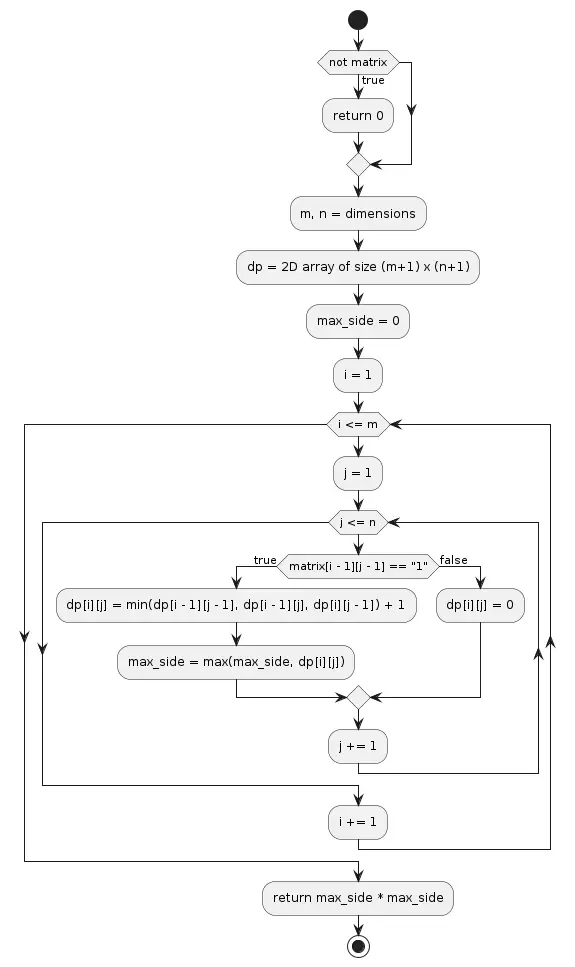
def maximal_square(matrix):
if not matrix:
return 0
m, n = len(matrix), len(matrix[0])
dp = [[0] * (n + 1) for _ in range(m + 1)]
max_side = 0
for i in range(1, m + 1):
for j in range(1, n + 1):
if matrix[i - 1][j - 1] == "1":
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
max_side = max(max_side, dp[i][j])
return max_side * max_side
# Test cases
test_inputs = [
([
["1", "0", "1", "0", "0"],
["1", "0", "1", "1", "1"],
["1", "1", "1", "1", "1"],
["1", "0", "0", "1", "0"]
], 4),
([
["1", "1", "1", "1", "1"],
["1", "1", "1", "1", "1"],
["1", "1", "1", "1", "1"],
["1", "1", "1", "1", "1"]
], 16),
([
["1", "1", "0", "0", "0"],
["1", "1", "0", "1", "1"],
["1", "1", "1", "1", "1"],
["1", "0", "1", "1", "1"]
], 4),
]
for matrix, expected_output in test_inputs:
result = maximal_square(matrix)
print(f"Input Matrix:")
for row in matrix:
print(row)
print(f"Output: {result}\nExpected Output: {expected_output}")
print("=" * 40)Exercise 6: Find Out Total Ways to Decode a String of Digits
A message is encoded into numbers where each digit corresponds to a letter (‘1’ -> ‘A’, ‘2’ -> ‘B’, …, ’26’ -> ‘Z’). Write Python code to find out the total ways to decode a non-empty string of digits.
Example:
Given the input "227," there are three possible decodings: "AZ" (2 possibilities), "BG" (1 possibility), or "BB" (1 possibility), resulting in a total of 3 possibilities.Solution:
def num_decodings(s):
if not s or s[0] == "0":
return 0
n = len(s)
dp = [0] * (n + 1)
dp[0] = dp[1] = 1
for i in range(2, n + 1):
if 1 <= int(s[i - 1]) <= 9:
dp[i] += dp[i - 1]
if 10 <= int(s[i - 2:i]) <= 26:
dp[i] += dp[i - 2]
return dp[-1]
# Test cases
test_inputs = [
("226", 3),
("12", 2),
("111", 3),
("0", 0),
]
for s, expected_output in test_inputs:
result = num_decodings(s)
print(f"Input String: {s}")
print(f"Output: {result}\nExpected Output: {expected_output}")
print("=" * 40)These exercises tackle a variety of algorithmic challenges, including dynamic programming and matrix manipulation. They encourage critical thinking and careful consideration of edge cases.
Let’s continue with a few more tricky and challenging Python exercises.
Exercise 7: Root-to-Leaf Paths with Target Sum in Binary Tree
Given a binary tree and a target sum, find all root-to-leaf paths where each path’s sum equals the target sum.
In a binary tree, a “root-to-leaf path” is the sequence of nodes you encounter while traversing from the root of the tree to a leaf node. A leaf node is a node that doesn’t have any children. For example, in the below tree, a root-to-leaf path could be: [1, 2, 4].
1
/ \
2 3
/ \
4 5Example
For the binary tree:
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1and target sum = 22, the paths are:
- [5, 4, 11, 2]
- [5, 8, 4, 5]
Solution
The solution involves depth-first traversal of the binary tree while keeping track of the current path and checking the sum at each leaf node.
class TreeNode:
def __init__(self, v=0, l=None, r=None):
self.v = v
self.l = l
self.r = r
def find_paths_with_sum(root, target):
def dfs(node, path, curr_sum):
if not node:
return
curr_sum += node.v
path.append(node.v)
if not node.l and not node.r and curr_sum == target:
res.append(path[:])
dfs(node.l, path, curr_sum)
dfs(node.r, path, curr_sum)
path.pop()
res = []
dfs(root, [], 0)
return res
# Test
root = TreeNode(5)
root.l = TreeNode(4, TreeNode(11, TreeNode(7), TreeNode(2)))
root.r = TreeNode(8, TreeNode(13), TreeNode(4, None, TreeNode(1)))
print(find_paths_with_sum(root, 22)) # Output: [[5, 4, 11, 2]]Exercise 8: Find the Minimum Window String (T) in String (S)
Given a string S and a string T, find the minimum window in S that contains all the characters of T in complexity O(n).
A Minimum Window String refers to the shortest substring of a given string that contains all the characters of another specified string.
So, in other words, you should look for a substring in S that has all the characters of T and is as small as possible. The complexity constraint O(n) means that you aim for an efficient linear-time solution.
Example
Input: S = "ADOBECODEBANC", T = "ABC"
Output: "BANC"Solution
The solution requires the sliding window technique and maintaining a frequency map of characters in the strings.
def min_win_sub(s, t):
if not s or not t or len(s) < len(t):
return ""
ct = {}
for c in t:
ct[c] = ct.get(c, 0) + 1
left, right = 0, 0
min_len = float('inf')
min_win = ""
req_chars = len(ct)
while right < len(s):
if s[right] in ct:
ct[s[right]] -= 1
if ct[s[right]] == 0:
req_chars -= 1
while req_chars == 0:
if right - left < min_len:
min_len = right - left
min_win = s[left:right + 1]
if s[left] in ct:
ct[s[left]] += 1
if ct[s[left]] > 0:
req_chars += 1
left += 1
right += 1
return min_win
# Test
print(min_win_sub("ADOBECODEBANC", "ABC")) # Output: "BANC"Exercise 9: Python Code for the Longest Subsequence Length
Given an unsorted array of integers, find the length of the longest increasing subsequence.
In an array, a “Longest Increasing Subsequence” is a sequence where each number is greater than the previous one. They don’t have to be next to each other, just always increasing.
Example
You have an array of numbers. Find the length of the longest subsequence where the elements are in increasing order.
Input: [10, 9, 2, 5, 3, 7, 101, 18]
Output: 4 (The LIS is [2, 3, 7, 101])Solution
The solution involves dynamic programming to find the length of the longest increasing subsequence.
def lst_len(nums):
if not nums:
return 0
n = len(nums)
dp = [1] * n
for i in range(1, n):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
# Test
input_nums = [10, 9, 2, 5, 3, 7, 101, 18]
print(lst_len(input_nums)) # Output: 5These Python coding exercises cover various aspects such as tree traversal, string manipulation, and dynamic programming. Each problem has a specific statement, example, and a brief description of the solution approach.
Exercise 10: Python Code to Check If a Sudoku Board is Valid
Determine if a 9×9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
- Each row must contain the digits 1-9 without repetition.
- Each column must contain the digits 1-9 without repetition.
- Each of the nine 3×3 sub-boxes of the grid must contain the digits 1-9 without repetition.
Example:
def is_valid_sudoku(board):
seen = set()
for i in range(9):
for j in range(9):
num = board[i][j]
if num != '.':
if (i, num) in seen or (num, j) in seen or (i // 3, j // 3, num) in seen:
return False
seen.add((i, num))
seen.add((num, j))
seen.add((i // 3, j // 3, num))
return True
# Test
sudoku_board = [
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
print(is_valid_sudoku(sudoku_board)) # Output: TrueThis exercise covers the validation of a Sudoku board, providing a mix of algorithmic challenges. Feel free to explore these problems again and again to boost your coding skills!
Some More Tricky Python Coding Exercises
40 Python Exercises for Beginners
Top 50 Python Data Structure Exercises (List | Set | Dict | Tuple)
Top 45 Python Exercises on Loops, Conditions, and Range() Function
30 Python Programming Questions On List, Tuple, and Dictionary
20 Problems On Concatenated Strings in Python with Solutions
Python Data Class Exercises for Beginners
20 Challenging Developer Pseudo Code Questions and Answers
Benefits of Python Tricky Coding Exercises
By attempting exercises like these, you build a robust foundation in algorithmic thinking and problem-solving. You will see several of the following benefits.
- Diverse Skill Set: Working on a variety of exercises you develop a diverse set of skills. These include algorithmic thinking, problem-solving, optimization, and logical reasoning.
- Coding Proficiency: Implementing solutions to such exercises improves your coding skills, helping you become a more proficient programmer.
- Interview Preparation: Many technical interviews for software engineering positions include similar types of problems. Practicing exercises like these prepare you for real-world problem-solving scenarios.
These are essential skills in the field of computer science and software engineering. They prepare you for both technical interviews and real-world challenges where analytical thinking and coding proficiency are crucial.
Happy coding!









